Proof 1
Proof that there are infinitely many primes
Prime numbers, the indivisible numbers, are the atoms of mathematics. The hydrogen and oxygen of the universe of numbers. Every number is built by multiplying these prime numbers together. For example 105 = 3 x 5 x 7. In Chemistry the Periodic Table lists finitely many atoms from which all matter is built. But what about prime numbers? It turns out that there are infinitely many primes in the mathematicians Periodic Table. To prove this requires showing why any finite list of primes cannot build all numbers.
Formal proof
A prime number is a number that is only divisible by itself and 1. Every number can be written as prime numbers multiplied together. The proof that there are infinitely many indivisible numbers works by showing that any finite list of primes cannot include them all. Suppose that you think that 2, 3 and 5 are all the primes you need to build all numbers. The trick is to multiply the primes in the finite list together (so in this case 2 x 3 x 5) and then the act of genius is to add 1 to this number (so we get 2 x 3 x 5 + 1). Which primes divide this new number? Well none in your list because the number has been built so you always get remainder 1 when you divide by a prime in the finite list. Therefore the list is missing primes. This proof works no matter how big the finite list of primes. It’s always missing some. So there must be infinitely many prime numbers.
Proof 2
Proof that the square root of 2 is irrational
If you draw a square with sides of length one unit then Pythagoras’s theorem implies that the diagonal across the square has length the square root of 2. But what is this length? The Pythagorean’s thought that there might be a fraction whose square is 2. But it turned out that there is no fraction whose square is 2. To prove this they used a classic trick in the mathematician’s arsenal: proof by contradiction. Suppose there is a fraction and then show why this leads to the contradictory conclusion that a number is both odd and even at the same time. This is impossible so the original assumption that the square root of 2 is a fraction must be wrong.
Formal proof
Let L be a number whose square is 2 and suppose that L is actually equal to a fraction
L = A/B.
We will prove that this leads to a contradiction therefore proving that L is irrational (which means it is not a fraction).
We can assume that one of A or B is odd. If they are both even we can keep dividing both top and bottom by 2 until one of the numbers becomes odd.
Since L2 = 2 it means that
A2/B2 = 2.
Multiply both sides by B2
A2 = 2 x B2.
So is A odd or even? Well A2 is even so A must be even because odd times odd is still odd. So A = 2 x N for some number N. Since A is even that means that B must be the odd number. But hold on…
2 x B2 = A2 = (2 x N)2 = 2 x 2 x N2
so we can divide both sides of the equation by 2 to get
B2 = 2 x N2.
Remember that we’d worked out that B was the odd number. So B2 is also odd. But the right hand side of this equation is an even number! So if L is expressible as a fraction it would imply that odd=even. That’s clearly absurd so our original assumption that L can be written as a fraction must have been false.
Proof 3
Proof of Thales’s Theorem that the diameter of a circle always subtends a right angle to any point on the circle.
Thales of Miletus is credited with being the first known author of a mathematical proof. He proved that if you take any point on a circle, join that point to the two ends of a diagonal across the circle then the angle you’ve created is an exact right angle. But how can you be sure? Why does it not depend on which point on the circle you choose? The proof works by using things we already know about triangles. In particular we know that the angles in a triangle add up to 180 degrees. But how can we use this to prove that the angle at the circle is always 90 degrees?
Formal proof
To prove Thales’s Theorem: draw a third line going from the point on the circle to the centre of the circle.
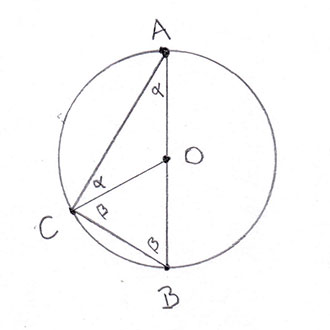
Why does this help? Now you have two triangles with two sides equal. This means the two angles opposite the centre of the circle are equal. Take the larger triangle you originally drew. Its angles add up to 2α + 2β. Combine this with knowledge that a triangle has angles adding up to 180 degrees then we know that α + β must be 90 degrees just as Thales asserted.
Proof 4
Proof that 1 + 1/2 + 1/4 + 1/8 + 1/16 + … = 2
If I take infinitely many fractions and add them together then you might expect the answer to be infinite. So why can I add up the numbers 1, 1/2 , 1/4 , 1/8 , 1/16 … and get the answer 2. Each number is half the size of the previous number. Think of a cake where I divide the cake in half. Now I divide one half in half again. Then divide one of these quarters into half again. I can keep dividing the pieces in half. Eventually I have infinitely many pieces, each half the size of the previous piece. And yet all the pieces add up to the whole cake I started with.
Formal proof
Let N be the number we get when we add up the infinitely many fractions
1 + 1/2 + 1/4 + 1/8 + 1/16 + …
We start by writing down an expression for 2 x N. Multiplying each of the numbers in our infinite sum by 2 we get
2 x N = 2 x (1 + 1/2 + 1/4 + 1/8 + 1/16 + …)
= 2 + 2 x 1/2 + 2 x 1/4 + 2 x 1/8 + 2 x 1/16 + …
= 2 + 1 + 1/2 + 1/4 + 1/8 + …
Having doubled N if I now take N away I will be left with N again:
2 x N – N = N.
But something rather amazing happens when we look at what 2 x N is and take away N:
2 x N – N =
2 + 1 + 1/2 + 1/4 + 1/8 + …
‐ 1 ‐ 1/2 ‐ 1/4 ‐ 1/8 ‐ 1/16 ‐ …
= 2
Why is the answer 2? Because all the other bits in the first line got taken away by the things in the second line. Only 2 was left. So we’ve worked out what N is. N = 2.
Proof 5
Algorithm for finding the highest common factor of two numbers
If I have two numbers then there must be a biggest number that can divide into both these numbers. But how can I find such a number? The number is called the greatest common divisor of the two numbers. Euclid’s Elements includes the first example of something we call an algorithm which is a method to find this greatest common divisor. An algorithm is a universal method that works to find the answer regardless of the input. Our modern world is run by algorithms but the very first example is already in Euclid’s Elements.
Formal proof
Suppose you have two numbers M and N (and suppose N is smaller than M). How do you find the largest number that divides both of them? Start by dividing M by N and call the remainder N1. If N1 is zero then N is the largest number that divides them both. If N1 is not zero then divide N by N1 and call the remainder N2. If N2 is zero then N1 is the largest number that divides M and N. If N2 is not zero then we do the same thing again. Divide N1 by N2 and call the remainder N3. These remainders are getting smaller and smaller and are whole numbers so at some point one of these remainders must hit 0. When it does, the algorithm guarantees that the previous remainder is the largest number that divides both M and N.
For example if M = 36 and N = 15, then dividing N into M, the remainder N1 = 6. Dividing N1 = 6 into N = 15 we get the remainder N2 = 3. But now dividing N1 by N2 we get no remainder so N2 = 3 is the largest number dividing both 36 and 15.


