Animating Xenakis’ ‘Nomos Alpha’

Animating Xenakis’ Nomos Alpha

By Marcus du Sautoy

For many years I’ve been obsessed by a solo cello piece by Greek composer Iannis Xenakis. Entitled Nomos Alpha, the piece is a perfect fusion of my two passions: the mathematics of symmetry and contemporary music. To celebrate Xenakis’ 100^th anniversary I’ve been working with artist Simon Russell to create an animation to guide listeners (and players) through the piece.

Nomos Alpha is dedicated to three mathematicians who have contributed to the mathematical understanding of symmetry including Evariste Galois who developed an algebraic language for symmetry called group theory. It is a language I use every day as a research mathematician as I strive to create new symmetries in hyperspace.

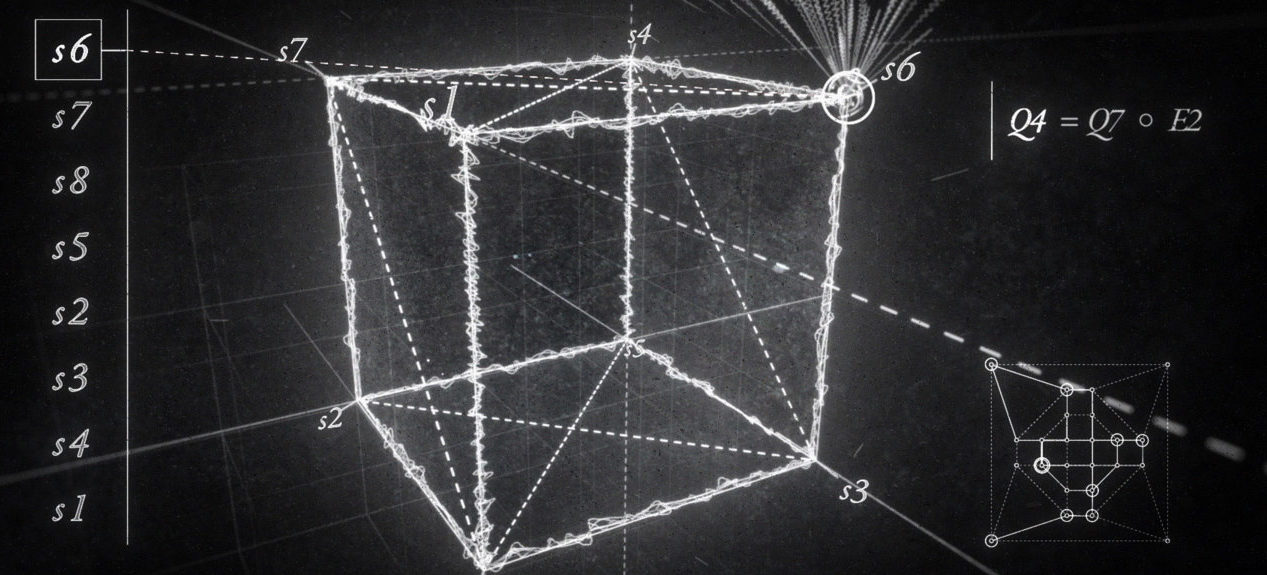
The cube, as seen in the ‘Nomos Alpha’ animation by Marcus du Sautoy and Simon Russell.

Xenakis’ composition is based on the symmetries of a very classical shape: the cube. There are 24 ways to rotate a cube from its starting position. Nine rotations of a quarter turn around the axis running through the centre of opposite faces. Six rotations of half a turn around an axis through opposite edges. And then eight rotations of a third of a turn around the axis through opposite corners. That makes 23 rotations but we mathematicians add another rotation which is just to leave the cube where it is. Like a zero rotation. That makes 24 rotations in total.

Nomos Alpha is divided into 24 sections. My immediate thought when I started exploring this piece is that there would be a section for each symmetry. However as I dug deeper into the piece I discovered something much more interesting is going on.

The piece is divided into 6 groups of 4 sections. The first 3 sections in each group correspond to 3 symmetries of the cube. The 4^th section is more fluid and imagines the cube morphing. Xenakis places 8 musical textures for cello on the corners of the cube, built out of pizzicatos, glissandi, tremolos and other techniques the cello can perform.

In each section these corners are played in a fixed order corresponding to two tetrahedra that can be embedded inside the cube. At the end of each section the cube then undergoes a rotation to rearrange the musical textures. The same path is mapped out in the new section but the textures are now played in a new order. A second cube keeps track of the time spent on each corner and the dynamics across the piece.

The fascinating thing for me is how Xenakis chooses the symmetries corresponding to each movement. He starts with two seed symmetries called D and Q12. D is a third of a turn through opposite corners. Q12 is a half turn through opposite edges. These control the first two sections. But to get the symmetry for the third section he rotates the cube using symmetry D and then rotates again using the symmetry Q12. The combined effect is a new arrangement that you can get in one go by doing symmetry Q4, a rotation of a quarter turn around an axis through opposite faces. For Xenakis each new symmetry is got by combining the two previous symmetries.

Iannis Xenakis and Le Corbusier. Source © el Hype 2022.

This immediately reminded me of the way the Fibonacci numbers are defined: 1, 2, 3, 5, 8, 13… You get the next number by adding the previous two numbers. These numbers are intimately related with growth in Nature and are beloved of artists especially architects. One architect in particular who loved weaving the Fibonacci numbers into his buildings was Le Corbusier. When Xenakis fled Greece to Paris in 1947 he spent 12 years working in Le Corbusier’s studio where he would have been exposed to the power of the Fibonacci numbers. It might have inspired Xenakis to experiment with this new idea of Fibonacci symmetries.

While the Fibonacci numbers spiral off to infinity, the Fibonacci symmetries eventually come back to the original two symmetries you started with and then repeat themselves. For the symmetries that Xenakis chooses in Nomos Alpha it takes 18 symmetries before the sequence repeats. This is the longest cycle of symmetries you can realise in the cube. If you choose two different seed symmetries then the sequence can be shorter so it is intriguing to know how much experimentation Xenakis did to discover this longest path. The 18 symmetries are not unique. Some of these symmetries are repeated twice.

Understanding the way that the symmetries of the cube control the structure of Nomos Alpha allowed me a way to listen to a piece that on my first encounter had felt very alien. I wanted to try to create a visual map of the journey the cello makes that would help other listeners coming to the piece for the first time to navigate its complexities. I also hoped that it might help those who already know the piece to listen to it in a new way and to assist performers who are learning the piece for the first time.

In the animation that I’ve made with Simon, the cube that is at the heart of creating the piece takes centre stage. At the beginning of each movement the cube rotates corresponding to the symmetry of the cube that controls that movement.  A label in the top right corner of the animation keeps track of the symmetry being played. The cello then plays the sound elements that are assigned to each corner of the cube. In our animation these are called S1, … , S8.

The path around these corners is the same for each movement and corresponds to two tetrahedron embedded in the cube. The sound elements are rearranged each time with the new symmetry corresponding to that movement. Every fourth movement sees the cube morphing and distorting corresponding to these freer sections. And then we are back to the next symmetry.

Each new symmetry is got by combining the previous two symmetries. We see this combination at work in the label keeping track of the symmetries. In addition there is a map mathematicians make of the symmetries of an object called the Cayley Graph. This map for the cube has locations for all 24 symmetries and the network depicts the way these symmetries are interrelated. Our animation keeps track of the path in the Cayley Graph that Nomos Alpha maps out through the 18 symmetries of the cube that it uses.

It was an exciting process to work with Simon creating this visual representation of Nomos Alpha. Simon and I have worked on a previous animation exploring the mathematics at the heart of Messiaen’s piece The Quartet for the End of Time which includes a fascinating use of prime numbers 17 and 29 in the piano part to create an interesting effect in the opening movement. This new animation has a very different character.

I was intrigued to ask Simon what the experience was like for him working on the piece, and below is his response:

“I knew close to nothing about the piece when I started so it was interesting to start to uncover the structures within it (with Marcus’ help!). It reminded me a lot like modern generative artwork driven by code. Where artworks are created with a set of relatively simple instructions with the aim of creating interesting variations and emergent properties. But it was interesting as well because it was not computer-based but relied on human interpretation.

I enjoyed the piece too because it was uncompromising, it felt really curiosity driven. It felt like Xenakis really just stayed true to the initial concept and saw how it unwound.

The challenge in producing the animation was in the scale of the piece. Twenty minutes is a long time in animation. I had to take Marcus’ detailed transcriptions of the order of rotations and convert them into a usable format for my 3D animation software. Once the 3D was done I had to create the textures and grains of the final piece as well as automate the diagrams and text overlays.”

Cellist Arne Deforce performing ‘Nomos Alpha’ as part of the world premiere of du Sautoy & Russell’s animation, Birmingham, 29 May 2022.

I also benefited from wonderful conversations with colleagues at PRiSM at the RNCM. Trying to explain how I was going to try to realise the visuals to help explain the composition was crucial in honing in on the best way to explain the complex ideas. We are grateful for PRiSM’s support through Research England E3 funding without which we would never have been able to realise such a rich visual celebration of this wonderful piece.

We premiered the animation at a special day dedicated to Xenakis on the 100th anniversary of his birth organised by the Birmingham Contemporary Music Group. The recording that we used for our online version of the piece is one made by the wonderful cellist Arne Deforce in 2011. We were very lucky that Arne agreed to join us for the day in Birmingham to perform Nomos Alpha live with our animation projected onto a big screen behind him.

I had the interesting challenge of matching the live performance to the fixed animation we had made. I decided to split the animation into 24 movements that I could trigger each time Arne hit that point in the score. In this way the hope would be that the shorter animations for each movement would match Arne’s performance. The only trouble is that Arne’s performance has evolved since his recording in 2011 and he is exploring taking the piece at a much faster pace. So I was frustrated in the first performance that the visual shifts through the corners of the cube did not match the aural shifts that Arne was making.

To solve this I realised I actually had to break the animation into 150 micro animations, corresponding to each corner being played in each of the movements controlled by a symmetry of the cube.

I was keen to give the live performance another go. I had been invited to speak about mathematics and music at the Boyne music festival in Ireland in July 2022. I asked cellist Julie-Anne Manning, one of the founders of the festival, whether she would be up for learning the piece so that she could perform it together with the animation. I was thrilled when she agreed to take up the challenge. It would also test my hope that the animation might help a cellist learning this piece for the first time.

I was intrigued to know how our work had affected her performance. She told me:

“The animation helped to bring to life the architecture of Xenakis’ Nomos Alpha. Although I can’t say I understand all of the mathematics, the structure and relationship between the sounds and the different apexes of the cube became more obvious. It’s fun and interesting to perform the work whilst seeing the audience following along on their mathematical journey.”

The performance of the piece, with Julie-Anne on cello and me triggering the visuals as she played through the corners of the cube, felt more like a duet than a solo. I was on stage with Julie-Anne with a music stand following the score like a hawk so that I knew when to trigger each new animation as Julie-Anne moved through the piece. A duet for cello and VJ.

Marcus du Sautoy in duet with Julie-Anne Manning in the last movement of ‘Nomos Alpha’.

The performance literally became a duet when we encountered the last movement. This last movement is the sixth in which we hear and see the cube morphing. In the previous morphing cube movements, the bottom C string of the cello has to be tuned down an octave. This is often solved in performance by having a second cello with the string already retuned which the performer can pick up to play.

The last movement however has two lines of music that the cellist is required to play. One line ascends into the heavens while the second line descends into the bass of the cello.

Simply put, it is impossible for a single cellist to physically play.

There are different ways to solve this challenge. In the performance with Arne in Birmingham he pre-recorded one line which was played from a speaker under his chair while he played the second line live.

In our performance in Boyne we found a second solution. I am an amateur cellist so as we reached the final movement I picked up the second cello on stage and as the animation unfolded we played the final movement as a duet.

Julie-Anne and I have had the chance to repeat our duet for cellist and VJ at a day organised by the South Bank Centre in London to celebrate the anniversary. The Xenakis community were very excited to see the work that we’ve done to reveal the secrets behind this composition. I am very hopeful that we will find further opportunities to share this incredible piece with audiences and guide them through the music with the help of our animation.

Perhaps the most intriguing result of this work though is that it has stimulated new mathematical research in my own practice. The idea of a Fibonacci sequence of symmetries is not something that has ever been considered in mathematics. It is a new idea that Xenakis contributes. I have been very intrigued to explore for other symmetrical objects what the maximal length of these Fibonacci loops in the group of symmetries can be.

For the cube Xenakis discovered that the maximum loop length is 18 but what about other shapes? Are there any patterns to the numbers? Is there a way to predict the lengths of the loops?

Xenakis’ piece Nomos Alpha has set me off on a new mathematical journey. Often mathematics inspires music but here we see music inspiring new mathematical ideas.